Interpolation und Approximation
In der Praxis werden häufig Näherungsverfahren, Interpolation wie Approximation, benötigt.
Die Ausgangssituation ist, dass für eine, empirisch oder analytisch ermittelte, Anzahl von Stützstellen
eine Funktion gesucht wird, welche die vorhandenen Datenpaare möglichst gut beschreibt.
In MasterAllRound sind zur Lösung dieser Aufgabe ausgewählte Interpolationsverfahren und
Approximationsfunktionen implementiert.
Dadurch sind Sie in der Lage, schnell und ohne Mühe, die für Ihr Problem geeignete Näherungsfunktionen
zu ermitteln.
Interpolation
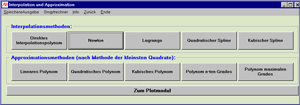
Von einer Interpolationsfunktion wird gefordert, dass sie an den Stützstellen gleich dem gegebenen Funktionswert ist und an den Zwischenstellen hinreichend gut Funktionswerte liefert. Folgende Interpolationsmethoden stellt MasterAllRound zur Verfügung:
- Direktes Interpolationspolynom
- Newtonsches Interpolationsverfahren
- Lagrangesche Interpolationsformel
- Quadratischer Spline
- Kubische Spline
Approximation
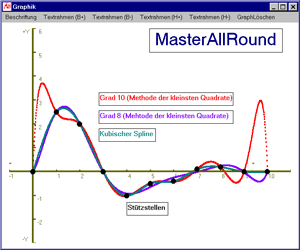
Eine Approximationsfunktion soll sich zwar möglichst gut an die jeweils vorgegebenen Werte annähern, es wird aber nicht gefordert, dass sie an den Stützstellen mit den Funktionswerten übereinstimmt.
Folgende Näherungsverfahren nach der Methode der kleinsten Quadrate stellt MasterAllRound zur Verfügung:
- Lineares Polynom
- Quadratisches Polynom
- Kubisches Polynom
- Polynom n-ten Grades
- Polynom maximalen Grades
MasterAllRound Merkmale
- Die Eingabe ist eine Textdatei mit den Wertepaaren
- Die Interpolationspolynome wie auch die Approximationsfunktionen werden als Textdatei gespeichert
- Die berechneten Funktionen werden ins Plotmodul übertragen
- Interpolation und Approximation ist zur graphischen Ausgabe direkt an das Plotmodul angebunden
|
English